Given: F(A, B, C, D) = (0, 2,4, 6,8,10,14). Use Karnaugh map to
Von einem Mystery-Man-Autor
Last updated 04 Juni 2024
Given: F(A, B, C, D) = (0, 2,4, 6,8,10,14). Use Karnaugh map to reduce the POS form. Write a logic gate diagram for the reduced POS expression.

Solved Simplify the following functions using a K-map and

Introduction of K-Map (Karnaugh Map)

Introduction of K-Map (Karnaugh Map) - GeeksforGeeks

Given the Boolean function F(A, B,C, D,) = ∑(2, 3, 6,7,8,10,12, 14, 15). Reduce the above expression by using 4- variable Karnaugh map, showing the various groups (i.c., octal, quads and pairs.

Given the Boolean function F(A, B,C, D,) = ∑(2, 3, 6,7,8,10,12, 14, 15). Reduce the above expression by using 4- variable Karnaugh map, showing the various groups (i.c., octal, quads and pairs.
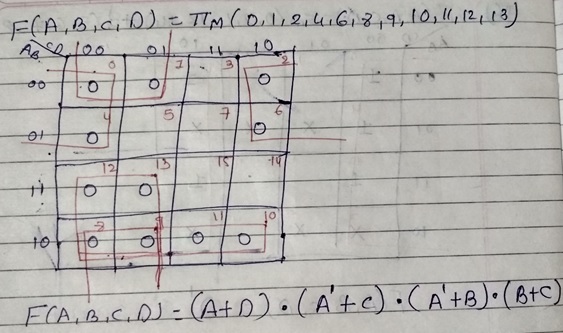
Simplify following function using k-map. F=Σ(1,2,3,4,6,8,9,10,11,12,14 )

Q. 3.4: Simplify the following Boolean functions, using Karnaugh maps: (a) F (x,y,z) = sum(2,3,6,7)
How to simplify following function using K-Map in SOPs form F (A,B, C,D) =∑ (1,2,3,8,9,10,15) - Quora

a) Find a minimum two-level NOR-gate circuit to realize $F_

Solved 8. Find the minimum sum-of-products expression for

Solved Use K-map to find the minimal SOP or POS expressions
für dich empfohlen
 Numerical fraction 6/414 Jul 2023
Numerical fraction 6/414 Jul 2023 How Big is a 4×6 Photo?(Inch, cm, mm, Ft, Pixels) - PhotographyAxis14 Jul 2023
How Big is a 4×6 Photo?(Inch, cm, mm, Ft, Pixels) - PhotographyAxis14 Jul 2023 How to Make Coffee Using the 4:6 Brewing Method – Philocoffea14 Jul 2023
How to Make Coffee Using the 4:6 Brewing Method – Philocoffea14 Jul 2023- Prayer can eradicate anxiety and bring peace of mind - Philippians14 Jul 2023
 Baby Development at 4-6 Months - Children's Hospital of Orange County14 Jul 2023
Baby Development at 4-6 Months - Children's Hospital of Orange County14 Jul 2023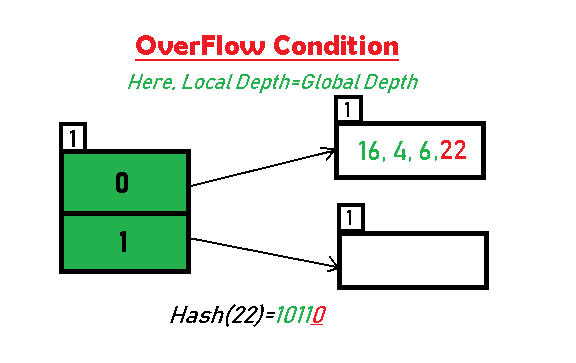 Extendible Hashing (Dynamic approach to DBMS) - GeeksforGeeks14 Jul 2023
Extendible Hashing (Dynamic approach to DBMS) - GeeksforGeeks14 Jul 2023 Pretty 6 Times table Chart - Print for free (many colors)14 Jul 2023
Pretty 6 Times table Chart - Print for free (many colors)14 Jul 2023- Artificial Christmas Trees, Prelit & Unlit Trees14 Jul 2023
 v60 4:6 Method Pour Over14 Jul 2023
v60 4:6 Method Pour Over14 Jul 2023- Jual CETAK PAS FOTO 2×3, 3×4, 4×614 Jul 2023
Sie können auch mögen
 File:BMW logo (white + grey background circle).svg - Wikimedia Commons14 Jul 2023
File:BMW logo (white + grey background circle).svg - Wikimedia Commons14 Jul 2023 Spoiler Cap Ford Kuga ST-Line Mk3 Our Offer \ Ford \ Kuga \ MK314 Jul 2023
Spoiler Cap Ford Kuga ST-Line Mk3 Our Offer \ Ford \ Kuga \ MK314 Jul 2023 Personalisierter Schlüsselanhänger aus Leder mit Gravur - sueco14 Jul 2023
Personalisierter Schlüsselanhänger aus Leder mit Gravur - sueco14 Jul 2023 Black Metal Mesh Top | The Life of the Party14 Jul 2023
Black Metal Mesh Top | The Life of the Party14 Jul 2023 Edelstahl Schneidringverschraubungen Zubehör Verschlusskegel - heco14 Jul 2023
Edelstahl Schneidringverschraubungen Zubehör Verschlusskegel - heco14 Jul 2023 Stroboskoplampe Zündlichtpistole14 Jul 2023
Stroboskoplampe Zündlichtpistole14 Jul 2023 Auto Abdeckung Abdeckplane Cover Ganzgarage outdoor Voyager für Audi , 99,78 €14 Jul 2023
Auto Abdeckung Abdeckplane Cover Ganzgarage outdoor Voyager für Audi , 99,78 €14 Jul 2023 2x ampoules LED Philips WY5W / W5W Oranges Ultinon PRO6000 - T1014 Jul 2023
2x ampoules LED Philips WY5W / W5W Oranges Ultinon PRO6000 - T1014 Jul 2023 Dekorative Autoleuchte HOODSHINE –14 Jul 2023
Dekorative Autoleuchte HOODSHINE –14 Jul 2023 Doppelseitige Klebepunkte - Ø 13 mm, 100 Stk.14 Jul 2023
Doppelseitige Klebepunkte - Ø 13 mm, 100 Stk.14 Jul 2023


